郑州市网站建设_网站建设公司_原型设计_seo优化
交换机的fault (发布与订阅模式)
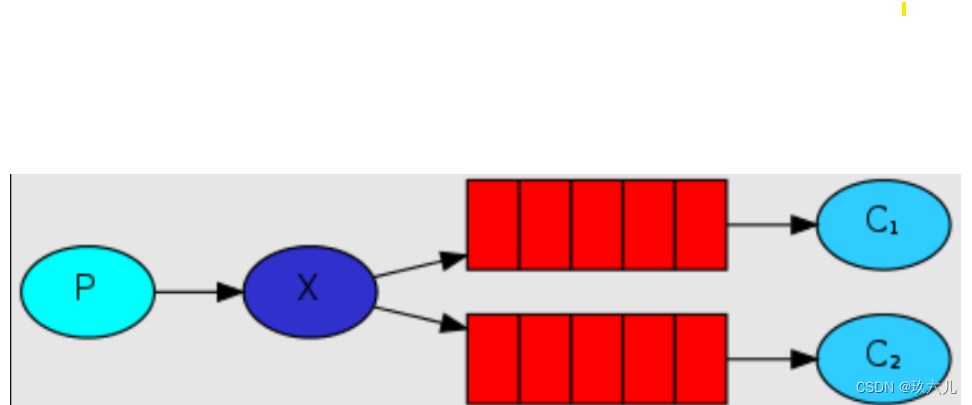
因为消息是由生产者发送给excahnge,exchange发送给队列, 然后由队列发送给消费者的。
展示使用图形化界面使用fanout模式。
创建交换机

然后创建三个队列,绑定对应的交换机,发现给交换机发送消息给队列, 3个队列同都收到了消息
direct模式
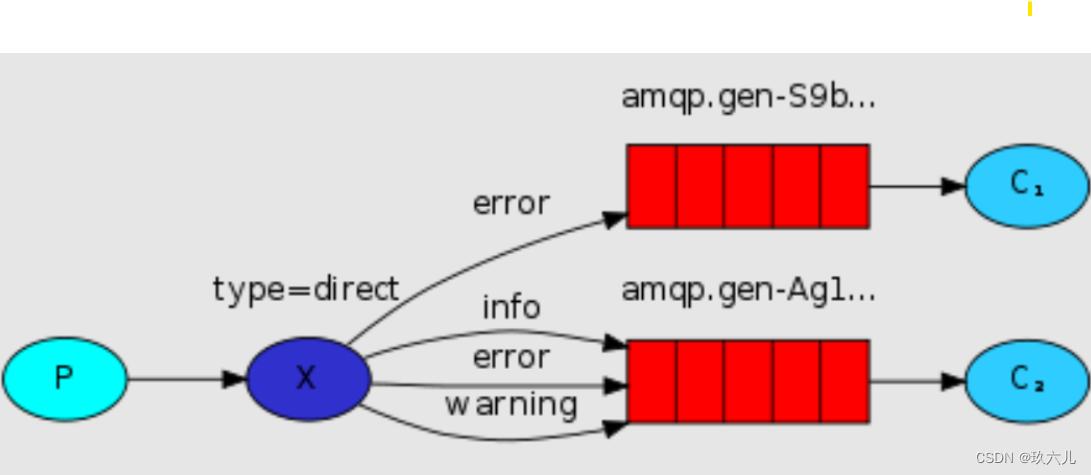
相对于发布订阅模式就是加了一个路由Key,如果说,消息的key是相同的,那么exchange就发送给对应的队列。
这个东西就像一个数据库, queue就相几张表, 交换机就往里面发数据。批量发,条件发。
和上面的一样,不过 使用 direct模式的交换机,可以指定路由key,也可以不指定路由key,
不过,如果是设置由
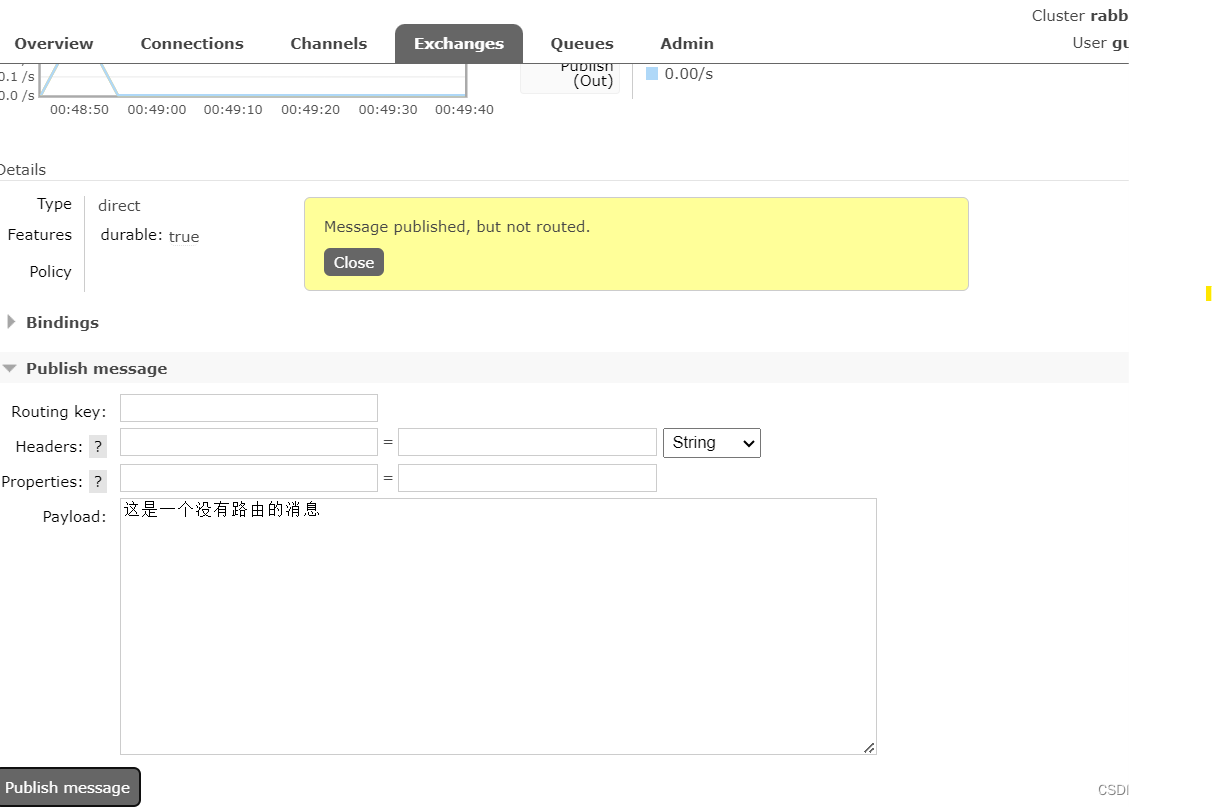
如果说是一个没有routKey的消息发送,那么就会发送给那些没有路由的队列
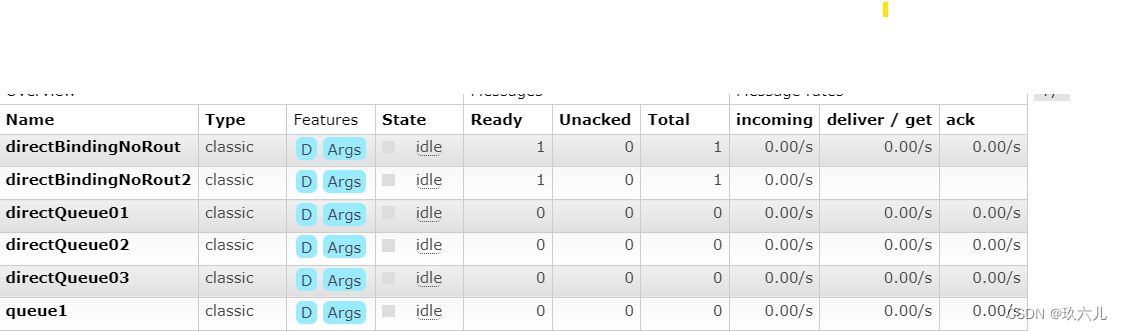
如果说 是由routkey的,那么就只会发送消息给那些 队列中由routkey的队列
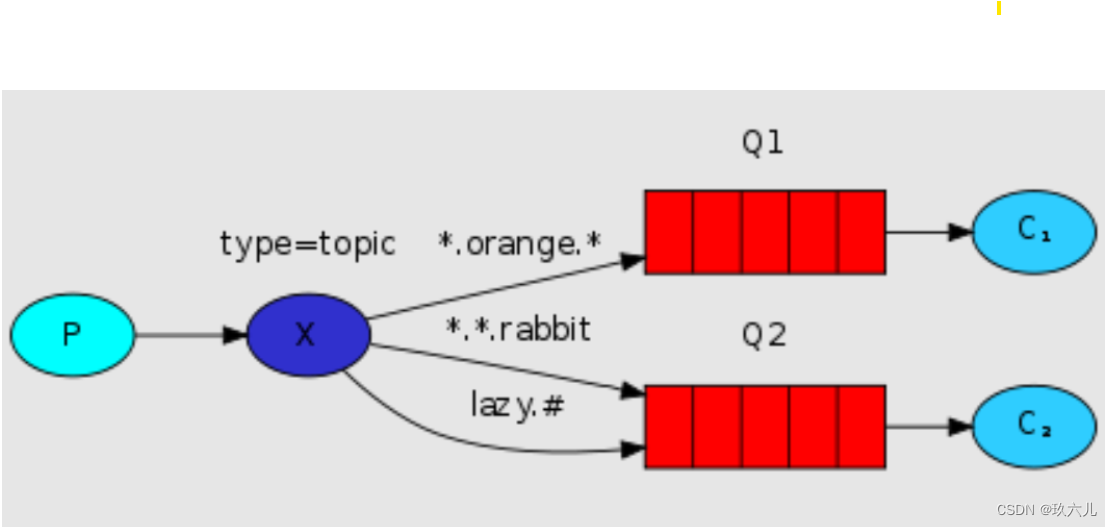
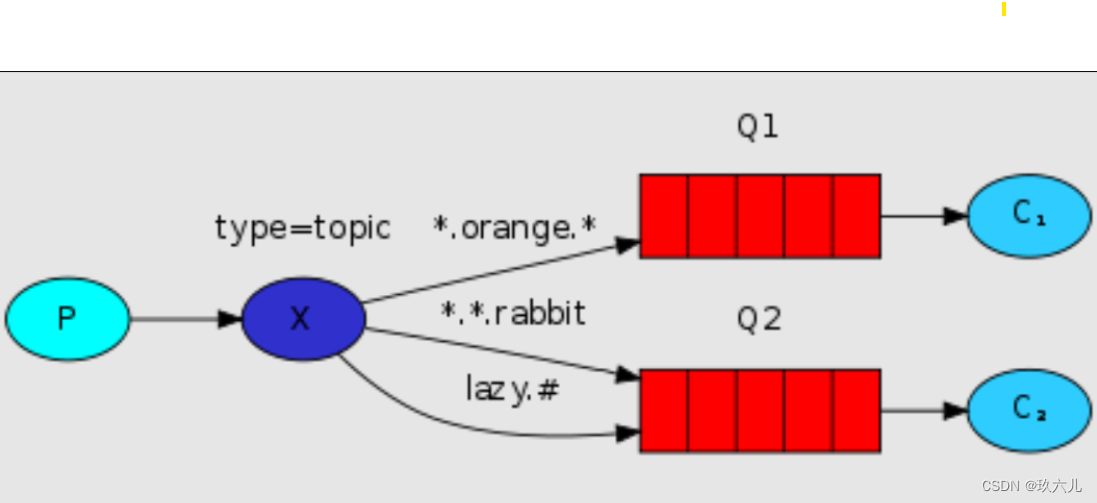
主题模式的交换机(topic)
可以看到主题模式相对于direct模式来说,添加了模糊匹配的路由规则
这里只是需要了解到 *的意思是一个,有且只有一个
#是一个或者多个。
headers的主题模式,带有参数的模式。
参数就是Arguments ,如果是代码的话就是props代表里面的参数显示。
上面的都是图形化的界面的显示。 下面使用springboot进行整合
fanout 发布订阅模式
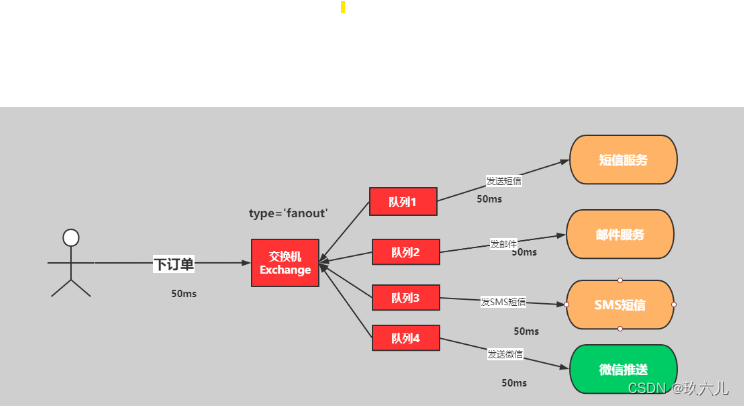
应用场景:
用户再下单之后相多个服务发送了短信推送服务、邮件服务、sms短信服务、微信推送服务
如果说在没有使用中间件的情况下,肯定是使用线程池,将每个消息都进行线程推送
但是这样 jvm中开启多个线程就十分的消耗资源,然后使用线程的过程中也是十分占用内存的资源,所以这个选择再开一台服务器,代替来工作,减少单台服务器的压力。
死信队列和过期时间的应用
这里只是 创建订单 -》做定时任务,超过10秒钟,将订单删除
如果说用户在这个时候支付了订单,可以将数据库中的支付状态改为 1 , 那么消息接收的时候判断支付状态:如果支付状态为1,那么就不删除,如果支付状态不为1,是0(表示未支付) 那么就不将订单删除。
或者,如果用户在这个时候支付了订单,那么同时将消息队列中的这个消息删除。
rabbitmq常见的问题:
1.如何保证消息消费的可靠性:
1)对于生产者:通过事物消息:对于本地来说,如果在进行一个业务的时候需要进行消息的发送,那么,将这个同时包裹为一个事物,这两个东西必须一块完成。(这里可以通过confirm方法判断消息是否发送成功),如果说投递失败了,可以放到重试队列中进行重试。
2)对于MQ本身,打开持久化,避免宕机出现消息的丢失。
3)对于消费者:改为手动应答机制ack,确认接收到了某个消息。
2.如何避免重复消费
避免不重复消费: 1)生产者:不进行重复投递
2)消费者:不进行重复消费,将消费过的消息放到redis中,接收到了消息之后判断在redis中有无,如果有的话,那么就是消费过了,如果没有,那么就进行消费。
这里的判断可以将消息进行组合加密成字符串,放到redis中。
3.如何保证顺序消费
单一消费者,但是对并发的效果不太友好。将需要保证顺序的进行hash,放到一组到同一个work模式。
4.如何实现延迟消息
一般使用死信队列。 本地存库,通过轮询。
5.消息为什么会堆积:
消费者消费的慢。 nack的多,可能有一直重发的。
或者再开一个topic服务。
