屯昌县网站建设_网站建设公司_轮播图_seo优化
1、如何验证MySQL数据库安装成功
按照上图操作打开SQL命令行客户端

输入安装MySQL时设置的密码并按enter键,得到下图:
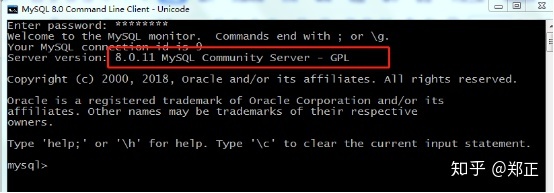
如果有显示出来红框里的内容,就表示安装成功。红框里的内容表示的是MySQL数据库版本号。
2、如何用客户端(Navicat)连接到MySQL数据库?
双击打开客户端Navicat,点击左上角连接按钮
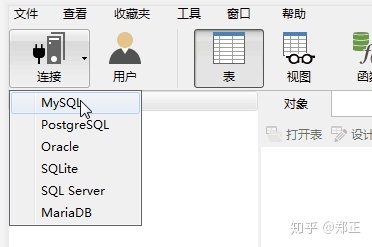
选择MySQL,弹出对话框,按下图填入数据库信息。(数据库信息一般是由提供数据库人员提供的)

点击连接测试,如果弹出连接成功按钮表示连接成功。
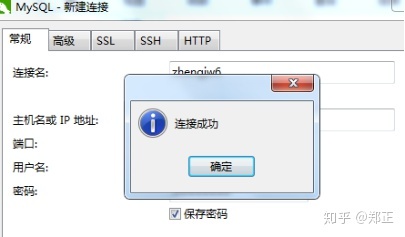
点击确定,即可看到连接成功的数据库。
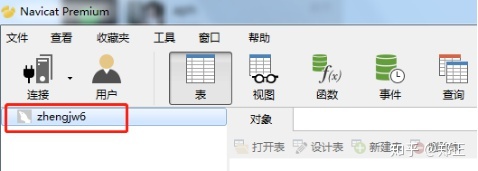
3、创建学校数据库的表
① 先创建学校数据库
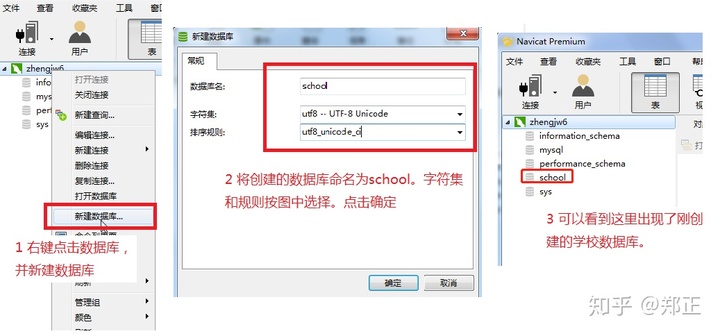
②在学校数据库里创建表
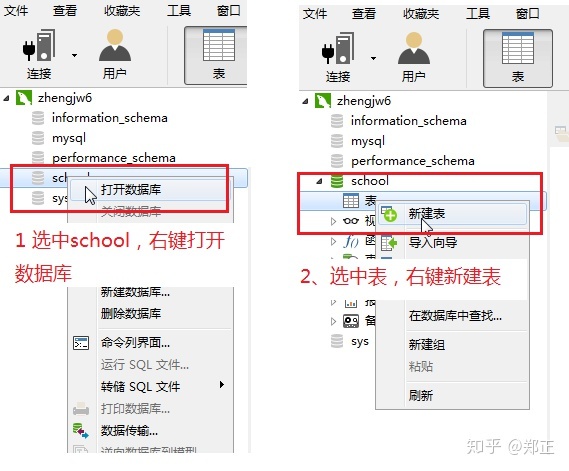
创建学生表:
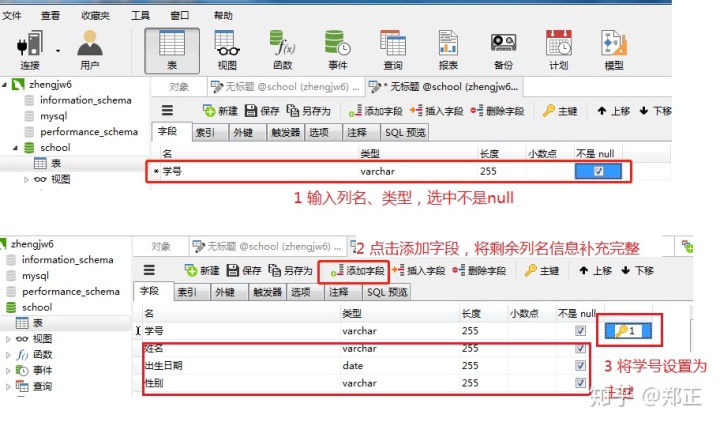
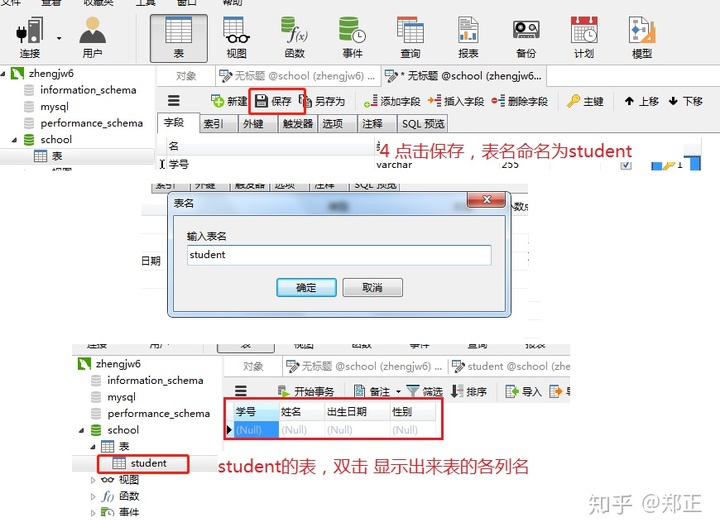
创建成绩表(步骤同上):
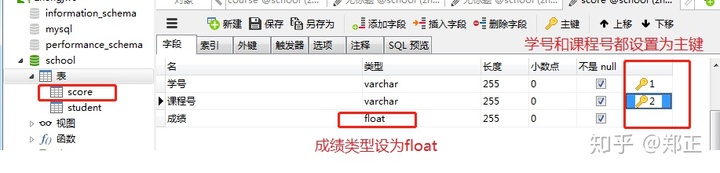
创建课程表:
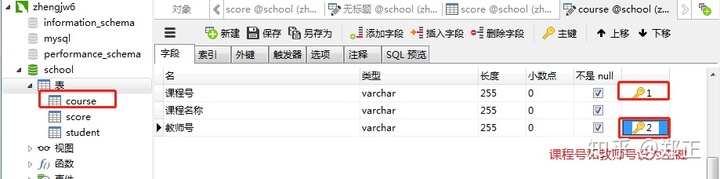
创建教师表:
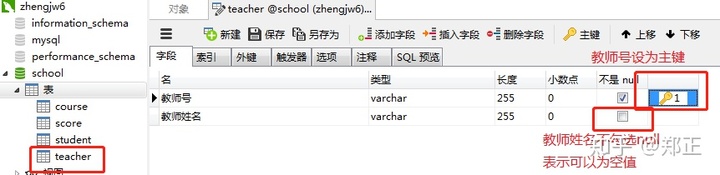
4、在上面创建的4个表里插入数据
①插入学生表数据
方法一:可以直接在客户端页面添加,适用数据较少的情况。
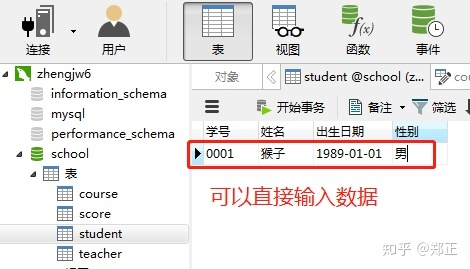
方法二:在客户端里输入添加数据的SQL进行添加
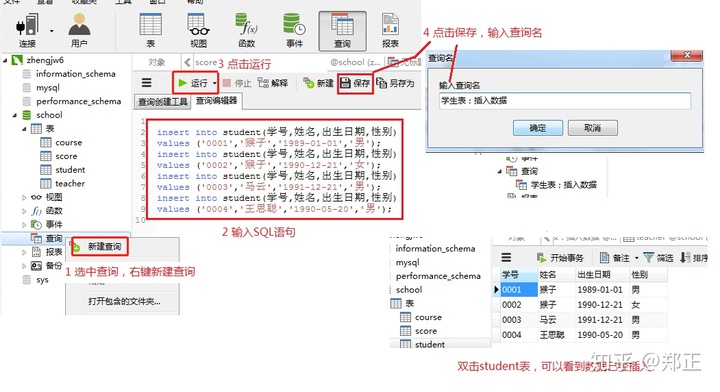
② 插入成绩表数据
通过客户端添加:
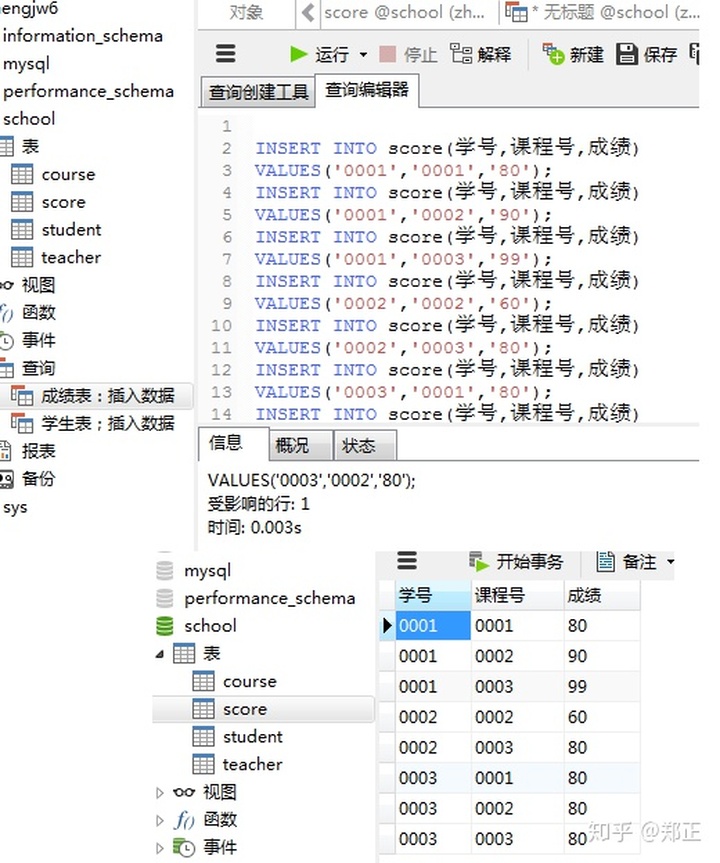
③插入课程表数据
通过客户端添加:
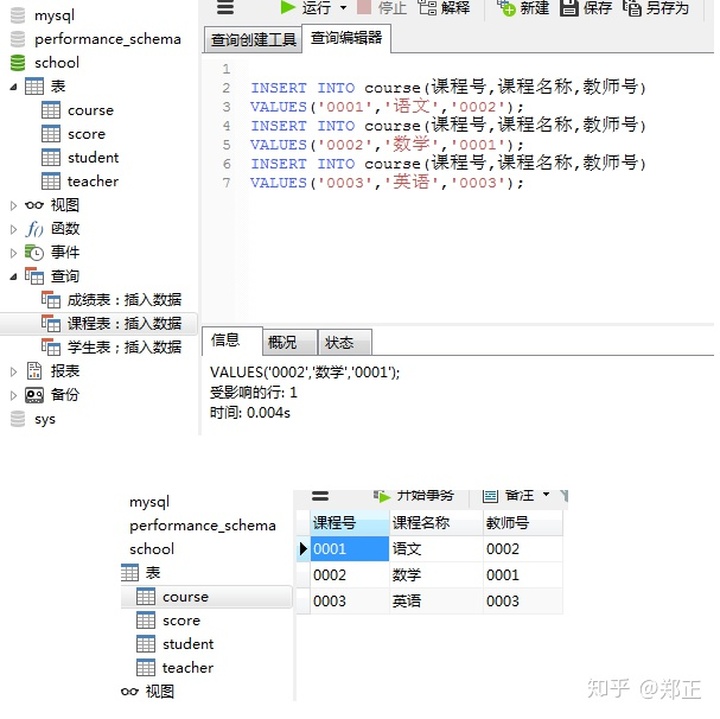
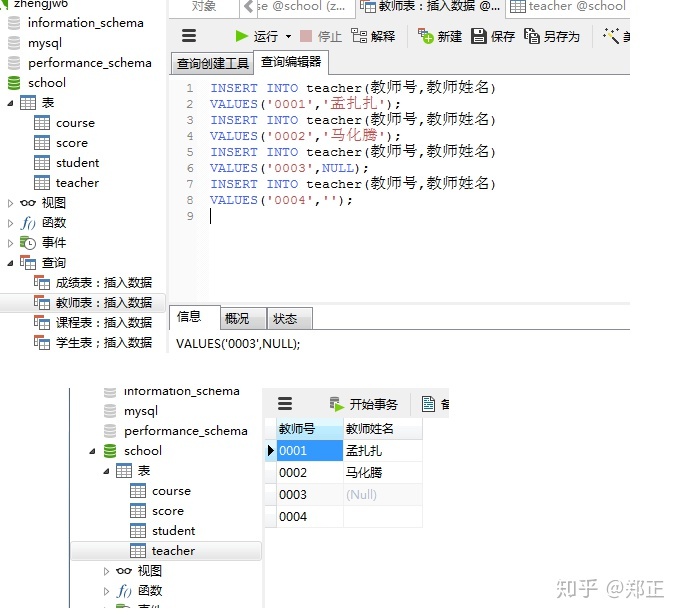
④插入教师表数据
通过客户端添加: