天水市网站建设_网站建设公司_SQL Server_seo优化
前言
响应模型我认为最主要的作用就是在自动化文档的显示时,可以直接给查看文档的小伙伴显示返回的数据格式。对于后端开发的伙伴来说,其编码的实际意义不大,但是为了可以不用再额外的提供文档,我们只需要添加一个 response_model=xxx,还是很爽的
示例
没有响应模型
from fastapi import FastAPI, Header
from pydantic import BaseModelapp = FastAPI()class Resp(BaseModel):code: intmsg: strdata: list@app.get("/")
async def read_root():return Resp(code=0, msg='success', data=[{"name": "Python"}, {"name": "Java"}])
效果
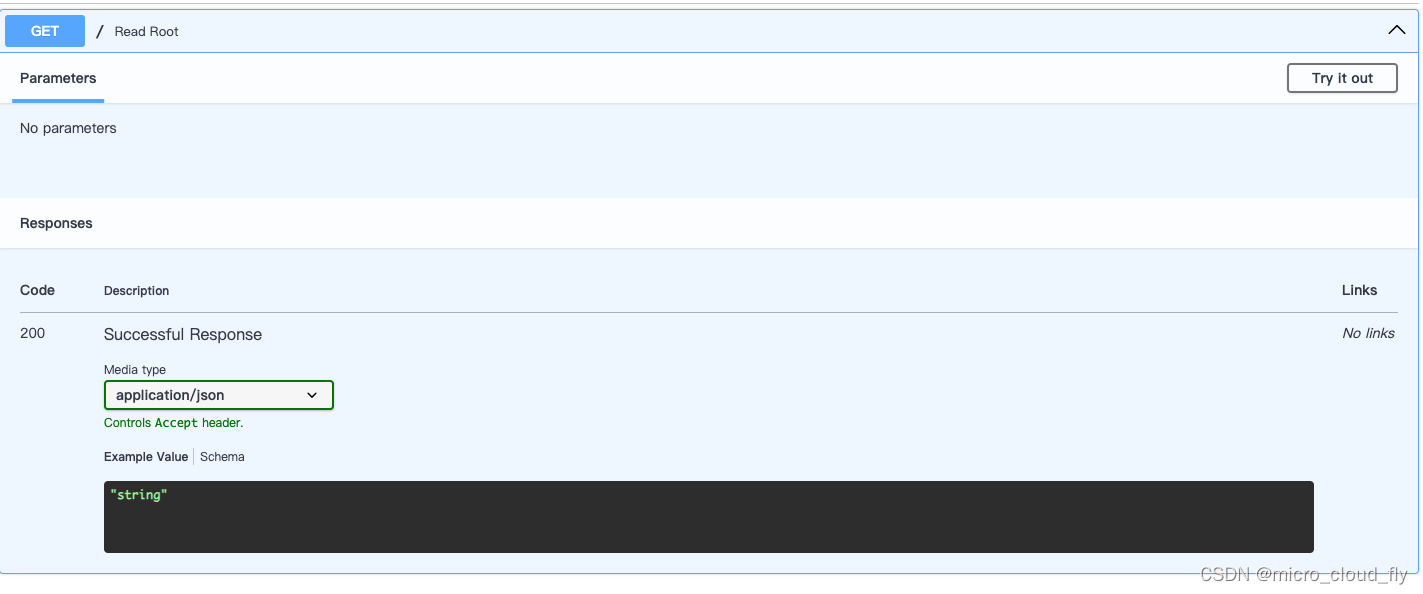
此时我们的文档只可以看到返回的是字符串,这和没写文档一样,现在尝试加上response_model
添加响应模型
from fastapi import FastAPI, Header
from pydantic import BaseModelapp = FastAPI()class User(BaseModel):id: intname: strclass Resp(BaseModel):code: intmsg: strdata: list[User]@app.get("/",response_model=Resp)
async def read_root():return Resp(code=0,msg='success',data=[User(id=1, name='test'),User(id=2, name='test2')])
打开自动化文档,显示效果如下:
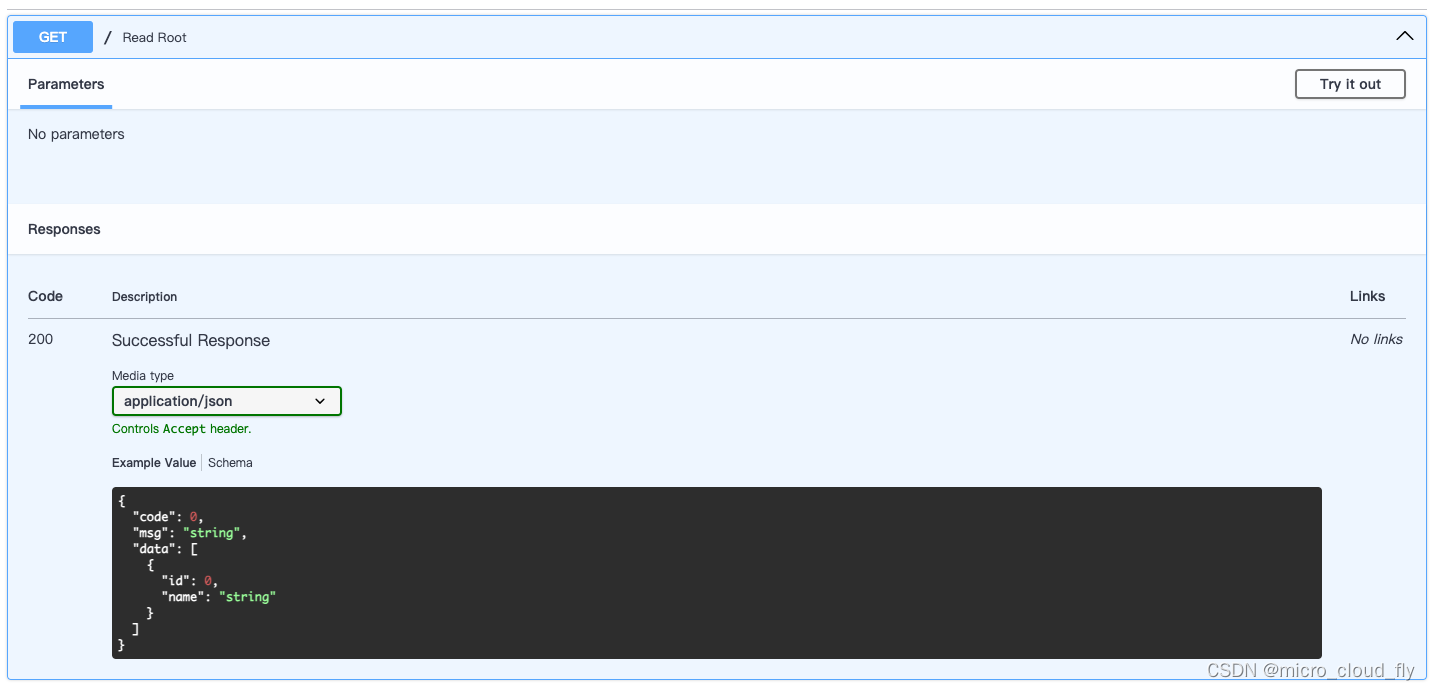
此时我们需要格外注意,我们规定了返回的是Resp模型,这个模型中有code、msg、data三个字段,如果我们返回的数据缺少了一个字段,那么,请求接口的时候,就会报错,比如我们把msg='success'注释掉,再次请求,将会有错误产生:

进阶使用:response_model_exclude_unset
如果你不想在响应模型中包括默认值未被修改的字段,你可以使用response_model_exclude_unset参数。
@app.post("/items/exclude_unset", response_model=Item, response_model_exclude_unset=True)
async def create_item_exclude_unset(item: Item):return item
在这个例子中,如果你提交了一个不包含description和tax字段的请求(因为它们有默认值且未修改),响应将不会包含这些字段。
response_model_include和response_model_exclude
response_model_include和response_model_exclude参数让你可以更精细地控制响应数据。response_model_include指定应该包含的字段,而response_model_exclude指定应该排除的字段。
只包含特定字段
@app.post("/items/include", response_model=Item, response_model_include={"name", "price"})
async def create_item_include(item: Item):return item
在这个例子中,响应只会包含name和price字段,即使其他字段在请求体中被定义。
排除特定字段
@app.post("/items/exclude", response_model=Item, response_model_exclude={"tax"})
async def create_item_exclude(item: Item):return item
在这个例子中,返回的响应将不包含tax字段。
实操演示
为了更好地理解这些概念,我们实现一个实例,其中我们创建一个简单的商品入库API,并在不同的端点展示response_model的不同用法。
from typing import Setfrom fastapi import FastAPI
from pydantic import BaseModelapp = FastAPI()class Item(BaseModel):name: strdescription: str = Noneprice: floattax: float = Nonetags: Set[str] = set()# 默认的response_model使用
@app.post("/items/", response_model=Item)
async def create_item(item: Item):return item# 排除未设置的字段
@app.post("/items/exclude_unset", response_model=Item, response_model_exclude_unset=True)
async def create_item_exclude_unset(item: Item):# 模拟item创建return item# 只包含特定字段
@app.post("/items/include_only", response_model=Item, response_model_include=["name", "price"])
async def create_item_include_only(item: Item):# 模拟item创建return item# 排除特定字段
@app.post("/items/exclude_some", response_model=Item, response_model_exclude=["tax"])
async def create_item_exclude_some(item: Item):# 模拟item创建return item
当你运行这个FastAPI应用并向这些端点发送请求时,你应该会注意到,每个端点都根据设定的参数,返回不同结构的JSON响应。
记得要调试和测试每个端点,确保它的行为符合预期,这样你就能更好地理解response_model的这些高级特性如何帮助你控制API的响应格式。
结论
response_model和其他相关参数提供了强大的方式来控制你的API响应。通过选择性地包括、排除或者隐藏响应数据的特定字段,你可以创建更加灵活和高效的API端点。这些特性尤其在处理大型数据模型或希望限制客户端收到数据的场景下非常有用。通过本教程的介绍,希望你能在自己的FastAPI项目中更加自如地使用这些高级功能。
